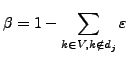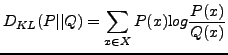 |
(1) |
Since this KL divergence is a non-symmetric information theoretical measure of distance of
![]() from
from ![]() , then it is not strictly a distance metric. During the past years, various measures
have been introduced in the literature generalizing this measure. We therefore have used the
following different symmetric Kullback-Leibler divergences i.e., Kullback-Leibler Distances (KLD)
for our experiments. Each KLD corresponds to the definition of Kullback and Leibler [13],
Bigi [4], Jensen [10], and Bennet [2] [27], respectively.
, then it is not strictly a distance metric. During the past years, various measures
have been introduced in the literature generalizing this measure. We therefore have used the
following different symmetric Kullback-Leibler divergences i.e., Kullback-Leibler Distances (KLD)
for our experiments. Each KLD corresponds to the definition of Kullback and Leibler [13],
Bigi [4], Jensen [10], and Bennet [2] [27], respectively.
KL and KLD have been used in many natural language applications like query expansion [8], language models [3], and categorization [4]. They have also been used, for instance, in natural language and speech processing applications based on statistical language modeling [9], and in information retrieval, for topic identification [5]. In this paper, we have considered to calculate the corpus document similarities in an inverse function with respect to the distance defined in Equations (2), (3), (4), or (5).
In the text clustering model proposed in this paper, a document ![]() is represented by a term vector of
probabilities
is represented by a term vector of
probabilities
![]() and the distance measure is, therefore, the KLD (the symmetric
Kullbach-Leibler divergence) between a pair of documents
and the distance measure is, therefore, the KLD (the symmetric
Kullbach-Leibler divergence) between a pair of documents
![]() and
and
![]() .
.
A smoothing model based on back-off is proposed and, therefore, frequencies of the terms appearing in the
document are discounted, whereas all the other terms which are not in the document are given an
epsilon (![]() ) probability, which is equal to
the probability of unknown words. The reason is that in practice, often not all
the terms in the vocabulary (
) probability, which is equal to
the probability of unknown words. The reason is that in practice, often not all
the terms in the vocabulary (![]() ) appear in the document
) appear in the document ![]() . Let
. Let
![]() be the vocabulary of the terms which do appear in the documents represented in
be the vocabulary of the terms which do appear in the documents represented in ![]() .
For the terms not in
.
For the terms not in ![]() , it is useful to introduce a back-off probability for
, it is useful to introduce a back-off probability for
![]() when
when ![]() does not occur in
does not occur in ![]() , otherwise the distance measure will
be infinite. The use of a back-off probability to overcome the data sparseness
problem has been extensively studied in statistical language modelling (see, for
instance [17]). The resulting definition of document probability
, otherwise the distance measure will
be infinite. The use of a back-off probability to overcome the data sparseness
problem has been extensively studied in statistical language modelling (see, for
instance [17]). The resulting definition of document probability
![]() is:
is:
with:
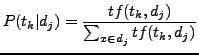
where:
![]() is the probability of the term
is the probability of the term ![]() in the document
in the document ![]() ,
, ![]() is a normalisation coefficient which varies according to the size of the document; and
is a normalisation coefficient which varies according to the size of the document; and
![]() is a threshold probability for all the terms not in
is a threshold probability for all the terms not in ![]() .
.
Equation 6 must respect the following property:
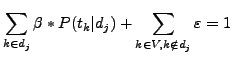
and ![]() can be easily estimated for a document with the following computation:
can be easily estimated for a document with the following computation: