Analysis of the unstability of TP

Although TP method obtained high $F$ values, it does not permits to decide the best quantity of terms to be used in a clustering task. It would be desirable to determine the best selection through an indicator based on characteristics of the collection. First of all, clustering method we have used has shown better performance when the number of clusters diminishes. This fact may be used in combination with $\bar{df_{V_i}}$, which is explained in the following paragraph.

Let $C_i$ be the text collection composed by the texts whose terms have been obtained by applying of TP method and including $i$ terms closer to $tp$ from each original text. Let $V_i$ be the vocabulary of $C_i$ and $\bar{df_{V_i}}$ the average of $df_t$ for terms $t$ that belong to $V_i$ but not to $V_{i-1}$. $\bar{df_{V_i}}$ value is linked to the similarity among the texts. Clearly lowest value of $\bar{df_{V_i}}$ is 1, and it means the new terms added to $V_{i-1}$ are not shared by the texts of $C_i$. In our experiments it was observed that a decreasing of $\bar{df_{V_i}}$ ( $df_{V_i}<df_{V_{i-1}}$) contributed to change instances from an incorrect cluster to a correct one. Therefore, terms with low $\bar{df_{V_i}}$ help to distribute texts into the clusters; the decreasing of $\bar{df_{V_i}}$, the decreasing of similarity between texts. Now, we can define an indicator of the goodness of a selection $C_i$.

Whenever the number of clusters ($N_i$) decreases after apply clustering to $C_i$, a lower $\bar{df_{V_i}}$ value means that new terms added to vocabulary $V_i$ will provide rising of similarity between texts in $C_i$. In such conditions $\bar{df_{V_i}}$ indicates a good selection. A way to express the above description is to say that a good clustering supposes that $\bar{df_{V_i}}$ be greater than $\bar{df_{V_{i-1}}}$ and $N_i$ be greater than $N_{i-1}$. We define the goodness of selection $C_i$ as:

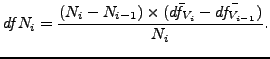$$dfN_i=\frac{(N_i-N_{i-1})\times(\bar{df_{V_i}}-\bar{df_{V_{i-1}}})}{N_i}.$$ (7)

In Table 3 a neighbour of maximum value of $dfN_i$ is shown. Row 1 is $i$, the number of terms selected by TP method, row 2 the size of vocabulary of $C_i$, row 3 normalized values of $dfN_i$, and in row 4 the $F$ measure.

Table 3: Some normalized values of $dfN_i$

i	20	21	22	23	24
$\vert V_i\vert$	1,572	1,619	1,661	1,706	1,744
$dfN_i$	0.573	0.621	1.027	0.584	0.990
$F$	0.637	0.6411	0.6415	0.636	0.551