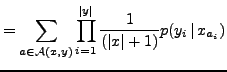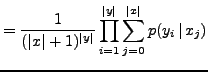Next: Maximum likehood estimation
Up: Using Query-Relevant Documents Pairs
Previous: Introduction
The QRDP probabilistic model
Lex 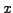 be a query text in a certain input (source) language, and let
be a query text in a certain input (source) language, and let
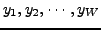 be a collection of
be a collection of 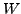 web pages in a different output (target) language. Let
web pages in a different output (target) language. Let
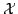 and
and
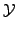 be their associated input and output vocabularies, respectively. Given a number
be their associated input and output vocabularies, respectively. Given a number
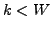 , we have to find the
, we have to find the 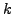 most relevant web pages with respect to the input query
most relevant web pages with respect to the input query 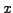 .
To do this, we have followed a probabilistic approach in which the
.
To do this, we have followed a probabilistic approach in which the 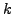 most
relevant web pages are computed as those most probable given
most
relevant web pages are computed as those most probable given 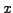 , i.e.,
, i.e.,
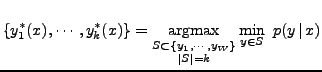 |
(1) |
In the particular case of k=1, Equation (1) is simplified to
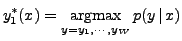 |
(2) |
In this work,
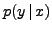 is modelled by using the well-known IBM alignment model 1 (IBM-1) for
statistical machine translation [6,11]. This model assumes that each word in the
web page is connected to exactly one word in the query. Also, it is assumed that the
query has an initial ``null'' word to
which words in the web page with no direct connexion are linked.
Formally, a hidden variable
is modelled by using the well-known IBM alignment model 1 (IBM-1) for
statistical machine translation [6,11]. This model assumes that each word in the
web page is connected to exactly one word in the query. Also, it is assumed that the
query has an initial ``null'' word to
which words in the web page with no direct connexion are linked.
Formally, a hidden variable
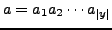 is
introduced to reveal, for each position
is
introduced to reveal, for each position 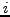 in the web page, the query
word position
in the web page, the query
word position
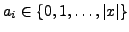 to which it is
connected. Thus,
to which it is
connected. Thus,
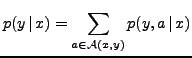 |
(3) |
where
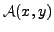 denotes the set of all possible alignments
between
denotes the set of all possible alignments
between 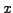 and
and 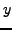 . The alignment-completed probability
. The alignment-completed probability
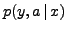 can be decomposed in terms of individual, web page
position-dependent probabilities as:
can be decomposed in terms of individual, web page
position-dependent probabilities as:
In the case of the IBM-1 model, it is assumed that
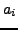 is uniformly distributed
is uniformly distributed
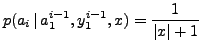 |
(6) |
and that 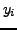 only depends on the query word to which it is connected
only depends on the query word to which it is connected
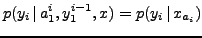 |
(7) |
By sustitution of (6) and (7) in (5); and thereafter
(5) in (3), we may write the IBM-1 model as follows by some straighforward manipulations:
Note that this model is governed only by a statistical dictionary
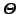 ={
={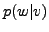 ,
for all
,
for all
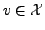 and
and
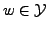 }.
The model assumes that the order of the words in the query is not important. Therefore, each position in
a document is equally likely to be connected to each position in the query. Although this assumption is
unrealistic in machine translation, we consider the IBM-1 model is particularly well-suited for our approach.
}.
The model assumes that the order of the words in the query is not important. Therefore, each position in
a document is equally likely to be connected to each position in the query. Although this assumption is
unrealistic in machine translation, we consider the IBM-1 model is particularly well-suited for our approach.



Next: Maximum likehood estimation
Up: Using Query-Relevant Documents Pairs
Previous: Introduction
David Pinto
2007-10-05
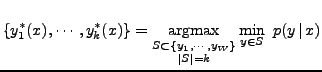
![]() is modelled by using the well-known IBM alignment model 1 (IBM-1) for
statistical machine translation [6,11]. This model assumes that each word in the
web page is connected to exactly one word in the query. Also, it is assumed that the
query has an initial ``null'' word to
which words in the web page with no direct connexion are linked.
Formally, a hidden variable
is modelled by using the well-known IBM alignment model 1 (IBM-1) for
statistical machine translation [6,11]. This model assumes that each word in the
web page is connected to exactly one word in the query. Also, it is assumed that the
query has an initial ``null'' word to
which words in the web page with no direct connexion are linked.
Formally, a hidden variable
![]() is
introduced to reveal, for each position
is
introduced to reveal, for each position ![]() in the web page, the query
word position
in the web page, the query
word position
![]() to which it is
connected. Thus,
to which it is
connected. Thus,
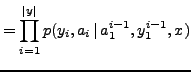
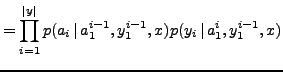
![]() is uniformly distributed
is uniformly distributed